Each fan has only one design point which is established by a specific air flow, total pressure, air density, and fan speed. Starting with these data, it is possible to determine one planform and the twist distribution which will accomplish the required work with minimum horsepower.

To move air, the fan must overcome two resistances, which are measured as pressure drops across the fan. The first is a parasitic loss called the velocity pressure loss and this is the energy required to move the required air quantity without doing any work to overcome the system resistance. Work is done however to move the hot air away from the equipment.

The second resistance is the static pressure loss. It is the accumulated losses due to inlet louver, fill, drift eliminator, and fan inlet pressure drop, etc. This would be the work to be accomplished and reflects the design of the total system. Whether the air is distributed evenly across the fan is primarily a function of the blade and hub design. A properly designed blade will have adequate chord width and twist to ensure an even distribution of velocity pressure over its entire length. A properly designed hub will include a center air-seal disk which prevents negative air flow into the center of the fan. Following are two cases that most everyone has faced;

• Designing a new tower from sketch, attempting to get the best design possible.
• Replacing a fan on an old tower where practically nothing is known.

What we are seeking in the brand new selection procedure is an optimum fan diameter, number and type of blades, required pitch angle, fan rpm, and some estimate of horsepower. In some cases we are looking for an estimated sound-pressure level to satisfy EPA requirements for working area noise levels, more importantly noise level at a plant boundary, or a given noise sensitive location such as a residential area.

A problem that arises frequently is a fan replacement for an old tower that practically has no design data available. In this case, the only approach is to calculate the curve horsepower that will allow for the actual gear ratio and approximate density. We are looking for a fan that at least will be an adequate replacement for the original fan. Selecting a Hudson fan to replace an existing fan is generally very simple. The factors that must be known when replacing a fan on an existing installation are:

• Fan diameter.
• Installed motor horsepower.
• Gear reduction ratio of gear reducer.
• Shaft size or gear reducer model.
• Some estimate of elevation above sea level of installation.

2) Fan Selection

In selecting an optimum diameter of fan, number of fan blades, type of blades, required pitch angle, fan speed, and some estimate of horsepower via the computer aid fan model selection program the following factors should be considered and provided.

(1)Fan Use : Induced or Forced Draft Cooling Tower
(2)Airflow Volume (acfm): A typical airflow volume by the diameter of fan is as below. The normal air velocity at fan inlet is 1,600 to 2,000 fpm and the air velocity must not exceed 2,100 fpm. This is a guide line for the optimum performance of fan. Excessive airflow may result in a waste of horsepower and in a high drift loss of water droplets through the fan cylinder.

(3) Diameter of Fan (ft) or Cross Sectional Area of Tower (ft²): The fan diameter has significant bearing on performance primarily because the diameter effects the magnitude of the velocity pressure which is a parasitic loss and the fan diameter effects the pressure capability of the fan. In our estimation, velocity pressure should fall in the range of 0.14 to 0.25 inch water (1,600 to 2,000 fpm at 0.068 lb/ft³) for optimum performance. Of course, other factors influence the choice of fan diameter, such as cell-size limitations, or selection of a fan for an existing installation.

Coping with a high velocity pressure requirement is just to add blades. However, this presents a good case for converting velocity pressure into useful static pressure capability by adding velocity recovery stack (called fan stack). The solidity ratio expressed by the ratio of the total width of the fan blades to the fan circumference is a way to compare a fan's pressure capability. The higher the ratio, usually the more work the fan can do. Still another aspect of optimum fan diameter is cost. Nonstandard sizes mean special handling by the fan maker at additional cost. (Standard fan diameter: 7, 8, 9, 10, 11, 12, 13, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32 in feet)

For a proper air distribution the area of fan coverage shall not be less than 30% of the cross sectional area of tower for the induced draft type of cooling tower and 40% for the forced draft type of cooling tower. Less fan diameter than these percentages will require more plenum chamber for enough mixing of air induced from the eliminators. Otherwise, the poor mixed air will generate the air turbulence, will make more vibration & noise, and will reduce the fan performance. Of course, the air will not be smoothly and evenly introduced into the fan from the drift eliminator.

(4) Actual Static Pressure (inch water): The total static pressure consists of pressure drops at the air inlet & louver, the fill, the eliminator, and the fan inlet. The pressure gain using the velocity recovery fan stack can be deducted from the total static pressure if you are using the different type of velocity recovery defined in Chapter 4 (Fan Stack, 7?of incline, 70% of efficiency, 0.08% of tip clearance, inlet shape of elliptic).

The calculation of pressure drops at the air inlet & louver, eliminator and fan inlet are so easy, while the pressure drop at fill can be read from the pressure drop curve (It depends on the air velocity, water loading, depth of fill and density of air, etc. with a specific model of fill.) The pressure drops at the air inlet & louver, eliminator and fan inlet can be generally obtained from a formula of K x 1/2 x (density x 0.1922) x (V²/115,820), where K is a pressure drop coefficient, 1g = 9.8016 m/sec² = 115,820 ft/min², and 1 lb/ft² = 0.1922 inch H₂O, whose K is in general 1.5 to 3.5 for the air inlet & louver, 2.0 to 3.0 for eliminator, and 0.1 to 0.35 for the fan inlet.

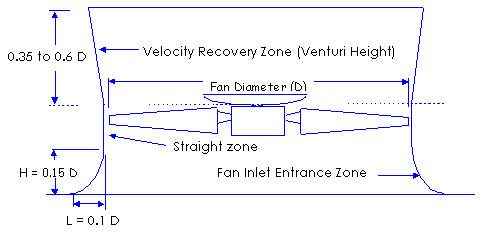
(5) Temperature at Fan (^oF) & Elevation of Site (ft) or Air Density (lb/ft³): This factor is very important in selecting the fans because of their effect on fan pressure capability and horsepower requirement through change in air density. This factor is combined into a density ratio. Hudson fan curve has a monograph for the density of dry air at 70? and sea level. The exit air of wet cooling tower is not simply a saturated air, but saturated air plus water vapor.

(6) Type of Fan Inlet Shape: Elliptical Inlet Bell (H/L = 0.15 x dia. of fan / 0.1 x dia. of fan) or what? Elliptical inlet shape proves to be ideal because the air flows along the wall with a uniform velocity and to the fan with the slightest possible turbulence. Other inlet shapes may be considered to add the extra resistance to the required duty point of the fan. The extra resistance may be determined with the aid of pressure loss factor. Also, the inlet shape influences the sound production of the fans.

(7) Venturi Height (ft) from Fan Plane to Top of Fan Stack : In the case of Wet Cooling Towers, a relatively common means of improving inlet conditions, conserving horsepower, and reducing the air recirculation into the air inlet is known as a fan stack. These stacks incorporate a slightly tapered exit cone and a well rounded inlet bell. In theory, there is a significantly reduced velocity pressure at the exit compared to the plane of the fan. Since the quantity of air is the same at both planes, the recovery of velocity pressure is converted into "static regain" which lowers the total pressure requirements of the fan, thus saving horse power. Below is a general shape of fan stack and is applicable for the actual cooling tower.

(8) Obstacle Area and Distance from Fan: (ft²/ft): The obstacles are mostly constituted by supporting beams, a gear reducer, and drive shaft, etc. These interference in the air flow due to obstacles located in the front of fan. Also, these obstacles cause a partial obstruction of the cross sectional area. As a result, extra losses occur. The losses depend on the ratio of total cross sectional area of fan casing to the obstacle area, and the ratio of the fan casing diameter to the distance from obstacles to the fan blade tip. Apart from a resistance increase in the air flow, obstacles cause an increase in sound production.

(9) Fan Speed (rpm), or motor full load speed & gear reduction ratio

(10) Fan Driver: Electric motor, speed control (single speed, two speed, or variable speed)

(11) Blade Pitch Control: Adjustable or variable pitch

(12) Number of Support Beam

(13) Minimum RF Margin (%): Details are described in Chapter 5.

(14) Required Noise Level (dB(A))

(15) Materials Construction of Tower Structure and Fan Stack: This is to be considered a maximum limit on the gear reducer itself not a normal level. Common practice in US is to use the minimum number of blades to reduce the vibration in the wood structure tower and FRP fan stack. This is to avoid dangerous air load induced pulsations on the fan cylinder. The fewer blades are occurring the higher air loads and are enlarging the more intense blade passing pulsation.

As a general rule, do not select the fans close to the limit of their BHP/blade. As bhp per blade = Brake Horse Power / Number of Blade, high blade air loading result in fatigue, vibration and noise problems. So, Hudson recommends the maximum per blade to be able to allow for fans as follows and 4 hp or less per blade is trouble free in most applications. These are guide line only and the minimum number of blades per fan would also be influenced by fan ring or fan stack rigidity or unusual loading conditions.
If the bhp/blade is excessive, you may:

• Increase the number of blades specified.
• Increase the fan diameter.
• Change to a wider chord blade type, if possible.
• Decrease the static pressure, if possible.

Let? look at a typical case of fan selection for a new cooling tower design. The following is a sample calculation for the thermal condition of 113.0 - 89.6 - 80.6?, 63,843 gpm of water flow, and induced draft counter flow type.

First and foremost, it is to decide the size of tower cell, air inlet height and depth of fill considering the heat load. The basic parameters for the optimum thermal design are as follows; the simplest way to design a new tower is to start with largest cell size and largest fan.

• 42' x 42' with a 28' fan, 175 hp (Square cell is best but rectangular tower with a ratio of length of width = 0.8 to 1.2, but all tower components are based on a 6' x 6' base increment.)
• Air inlet on 2 sides only & air inlet height 1/3 of cell width (In general, 1/4 to 1/3 to
  the cell width)
• Height of plenum chamber which is a distance between the top of eliminator and the bottom of fan deck is generally obtained from 0.25 x { (Tower Width² + Tower Length²)^1/2} - Fan Diameter } as minimum. Using a larger fan reduces fan power and reduces minimum plenum chamber height, but be careful: recirculation is likely to increase if fan discharge velocity is too low. If the less plenum is used to, the air velocity in the center part of the eliminators can become so high that the drift losses will occur. Same thing in the upper portions of the fill. All these result in the increased pressure drop, reduced airflow, and reduced performance.
• For the fill, use 4' (In general, 2' to 5' for film type of fill or 10' - 15' for splash fill)
• Water Loading: 2 to 14 US GPM/ft² for counter flow, 4 to 24 US GPM/ft² for cross flow
• Air Velocity at each location: The below is a guide line for the best performance with the minimum fan power. Especially the air velocity at the fill must be ranged in the below table. If the air velocity is low in the fill, the air can not be smoothly moved upward due to the restriction of downward water and if the air velocity is too high in the fill, the heat of water can not be completely removed as desired.
  
  The problem when the air speed at the air inlet exceeds below ranges is resulting in poor air distribution in the fill. For more details refer to the subjects of Air Distribution and Exit Velocity in Chapter 9, energy saving.

(1) Thermal Design Result: Considering the water and heat loading, 6 cells of 42' width x 42' length of tower size and 14' (33% or more to the width of tower cell) air inlet height is reasonable. For velocity recovery, 7^o of incline & 6.0' (21.4% to fan diameter) of venturi height was applied to this sample job. 1.0% fill support obstruction, without air inlet louver (10.0% air inlet obstruction), concrete structures.

(2) Airflow & Pressure Drop: The airflows and pressure drops at each location and each cell were produced as follows. Airflow is varying every location since the air volume is proportionally increasing as much as the heat of water is transferring into the air stream.

• Pressure Drop at Air Inlet & Louver = K x (1/2) x (density x 0.1922) x (V²/115,820)
  = 2.0 x (1/2) x (0.0717 x 0.1922) x (943.01²/115,820) = 0.1058 in H₂O
  
• Pressure Drop at Fill: This is given from the pressure drop curve of a specific model of fill. The fill area is a net area deducting the fill obstruction area from the total cross sectional area of 42' x 42' tower. That is, 10,478.16 ft² = 0.99 x 42' x 42 x 6 cells'. Note that heat transfer in this fill obstruction is not occurring since the water fraction and air stream can not be by-passed through the parts of fills to be just laid onto the fill supports. So, this area called "Dead Zone in Heat Transfer" must deducted as much as the fill obstruction percentage.
  
• Pressure Drop at Eliminator = K x (1/2) x (density x 0.1922) x (V²/115,820)
  = 2.0 x (1/2) x (0.0688 x 0.1922) x (608.77²/115,820) = 0.0423 in H₂O
  
• Pressure Drop at Fan Inlet = K x (1/2) x (density x 0.1922) x (V²/115,820)
  = 0.25 x (1/2) x (0.0688x 0.1922) x (1,853.71²/115,820) = 0.0491 in H₂O
  [Note that the net fan inlet area was obtained from pie/4 (Fan Diameter² - Seal Disc²). That is, 573.52 ft² = pie / 4 x (28² -7.3333²).]
  
• Velocity Pressure at Fan = (1/2) x (density x 0.1922) x (V²/115,820)
  = (1/2) x (0.0688 x 0.1922) x (1,853.71²/115,820) = 0.1963 in H₂O
  or Press. Drop = (V/4,008.7)² x 1/density ratio
  = (1,853.71/4,008.7)² x 1/(0.0750/0.0688) = 0.1963 in H₂O
  
• Velocity Pressure at Stack Exit = (1/2) x (density x 0.1922) x (V²/115,820)
  = (1/2) x (0.0688 x 0.1922) x (1,661.07²/115,820) = 0.1576 in H₂O
  or Press. Drop = (V/4,008.7)² x 1/density ratio
  = (1,661.07/4,008.7)² x 1/(0.0750/0.0688) = 0.1576 in H₂O
  [Note that the net fan stack exit area was calculated as per the formula of pie / 4 x {fan diameter + (2 x tan 7?x venturi height)}² - pie / 4 x (seal disc diameter)². That is, 640.03 = pie / 4{28 + (2 x 0.122785 x 6.0)}² - pie / 4 x 7.3333². The tip clearance was neglected for the venturi.]
  
• Velocity Recovery (Pressure Gain) = Efficiency of Fan Stack x VP at Fan x (1 - (Fan Dia. / Stack Exit Dia)⁴) 
  = 0.7571 x 0.1963 x (1 - (28 - 29.47)⁴) = 0.0276 in H₂O
  
  Since Hudson is considering 7?of stack incline and is neglecting the no air flow zone at the top stack due to the seal disc. (Unless the height of fan stack is as mush as the fan diameter, the area of seal disc in the fan must be subtracted from the fan stack top area. Refer to Flow Pattern, Chapter 4), the net fan stack area must be corrected to pie/4 x {fan diameter + (2 x tan 7^o x venturi height)}². The area obtained from this correction is 682.26 ft² and consequently the air velocity must be corrected to 1,558.24 fpm. Then, velocity recovery is obtained from 0.7 x (0.1963 - 0.1386 ) = 0.0404 in H₂0.
  
  Consequently, the fan brake horsepower based on above calculation can differ from Hudson? fan rating, since there is a little deviation in the velocity recovery. BHP per Hudson? fan rating program in case of inputting the 6.0' of venturi height and the 0.5100" Aq. of static pressure (not considering the 0.0276" of velocity recovery obtained from the thermal design result.) is 136.7HP. This is less than BHP when inputting 0.4825 Aq. of static pressure and not inputting the 6.0' of venturi height by 3.1 HP. So, this is a reason why we recommend the customers to use their own calculation on the velocity recovery due to the fan stack.
  
• Total Static Pressure: This is a value deducted by pressure gain, that is, velocity recovery from a summation of pressure drops at air inlet & louver, fill, eliminator and fan inlet.
  
  Total Static Pressure = (0.1058 + 0.3128 + 0.0423 + 0.0491) - 0.0276
  = 0.4825 in H₂O
  
• Total Pressure: This is a summation of Total Static Pressure and Velocity Pressure.
  
  Total Pressure = 0.4825 + 0.1963 = 0.6788 in H₂O

(3) Fan Diameter: As previously mentioned, the minimum fan coverage to the cross sectional area of each cell must not be less than 30% for the induced draft type of cooling tower or must not be less than 30% of the area of fill.

• Fan coverage to 30% of cross sectional area of 42' x 42' tower: 529.2 ft². This is equal to 25.96 ft.
• Fan coverage to 30% of net area of fill: 523.91 ft². This is equal to 25.83 ft.
  
  Judging from above fan coverage, 26' or 28' fan can be used. Considering fan shaft power, fan cost, fan stack cost, and allowable space in the fan deck, 28' fan is more applicable. As see the above airflow and pressure table, the air velocity at fan is less than 2,000 fpm. Accordingly, 28' of fan diameter is a best choice.

(4) Fan Speed: This must be fixed before deciding the number of fan blades, since the fan speed is directly corresponding to the fan brake horsepower and resonant frequency margin due to the change in the fan speed. If possible, it would be fine to select the fan speed considering the standard gear reduction ratio of manufacturers. If non-standard gear reduction ratio is used, the additional cost and delivery is requiring as usual. Model AGC-1712-14 in Amarillo? products is satisfying the mechanical power rating and gear ratio. Fan Speed = (Motor Full Load Speed / Exact Gear Reduction Ratio) = 1,770 / 14.000 = 126.4 rpm.

(5) Number of Fan Blades: This depends on the limitation of vibration at the gear reducer (i.e. material constructions), BHP/blade, fan speed, and minimum resonant frequency, etc. For maintaining the 80 micron of vibration at the position of gear reducer, the minimum 6 each of fan blade is required. However, this is exceeding the allowable BHP/blade (24 = max. BHP/blade - 4 hp = 24 - 4) for 28' fan. So, 6 blades of fan can not be used. Also, the pressure margin with 7 blades are too close to the critical operating line. Finally, the number of blade satisfying the allowable BHP/blade and the minimum 10% of pressure margin is 8 each.

(6) Automatic Selection: To optimum design the fan diameter & number of blades in accordance with the given airflow conditions, Hudson's fan rating program gives all the available fan diameter and number of blades based on the cost /hour. You can select a model having most less cost/hour, but it depends on the tower application designs. The operating cost/hour calculation is based on several variables:

• Fan Price Modifier: 1.0
• Asset Years: based on 10 years
• Work Hours/Year: based on 8,000
• Electric Power Cost: $0.46($/kw-hr)

But, you can calculate to modify the cost/hour using the following equation:

       (List Price x Price Modifier)       (Fan HP x 0.746 kw/hr) x (Cost/kw-hr)
--------------------------------------------------- + ----------------------------------------------------------
(Asset Years x Workhours / Year)                     Total Efficiency

Fan program is outputting all the available solutions for fan diameter and number of blade of fan on your given airflow conditions. For previous example, the result of solutions without information on the fan diameter and number of blades and under the conditions of;

• Fan use: included draft cooling tower
• Type of Blade: H Type
• Static pressure: 0.4825" Aq.
• Airflow: 1,063,126acfm
• Exit Air Density: 0.0688 lb/ft³
• Resonance Frequency Margin: 5%

Hudson's fan rating program outputs all the fan solutions for given airflow conditions. These solutions are all of the fan sizes and number of blades that meet the same airflow specifications, and their operating cost/hour values. If you absolutely do not want one of those fans, try with a different tip speed.