1) Hydrolysis of Chlorine Gas

When chlorine gas is dissolved in water, it hydrolyzes rapidly according to the following equation:

Cl₂ + H₂O <---> HOCl + H⁺ + Cl^-

Complete hydrolysis occurs in a few tenths of a second at 18^oC; at 0^oC only a few seconds are needed.

2) Chemistry of Hypochlorous Acid

The most important reaction in the chlorination of an aqueous solution is the formation of hypochlorous acid. This species of chlorine is the most germicidal of all chlorine compounds with the possible exception of chlorine dioxide. Hypochlorous acid is a weak acid which means that it tends to undergo partial dissociation as follows:

HOCl <---> H+ + OCl^-

to produce a hydrogen ion and a hypochlorite ion. In waters of pH between 6.5 and 8.5 the reaction is incomplete and both species are present to some degree. The table for the percent undissociated HOCl species for the various temperature and pH values is shown below.

The percent OCl^- ion is the difference between these numbers and 100. The percent distribution of the OCl^- ion (hypochlorite ion) and undissociated hypochlorous acid (HOCl) can be calculated for various pH values as follows:

Where, Ki is a constant of HOCl ionization and is calculated from (H⁺) x (OCl^-) / (HOCl). This constant is shown on below table.

At 20^oC and pH 8, the percent distribution of HOCl is obtained from;

100 x [ 1 + (Ki / H⁺) ]^-1 = 100 x [ 1 + (2.621 x 10^-8 / 10^-8) ]^-1 = 100 / 3.61 = 27.65%

HOCl is the most effective of all the chlorine residual fractions. This fraction is known officially in the industry as free available chlorine residual. Hypochlorous acid is similar in structure to water; hence, the formula HOCl is preferred to HClO. The germicidal efficiency of HOCl is due to the relative ease with which it can penetrate cell walls. This penetration is comparable to that of water, and can be attributed to both its modest size (low molecular weight) and to its electrical neutrality (absence of an electrical charge.)

Other things being equal, the germicidal efficiency of a free available chlorine residual is a function of the pH, which establishes the amount of dissociation of HOCl to H⁺ and OCl^- ions. Percent HOCl table shows the percentage of undissociated HOCl in a chlorine solution for various pH values an temperatures. Lowering the temperature of the reacting solution suppresses the dissociation; conversely, raising the temperature increase the amount of dissociation.

The rate of dissociation of HOCl is so rapid that equilibrium between HOCl and OCl^- ion is maintained, even though the HOCl is being continuously used. For example. if water containing 1 mg/l of titable free available chlorine residual has been dosed with a reducing agent that consumes 50 percent of the hypochlorous acid, the remaining residual will redistribute itself between HOCl and OCl^- ion according to the values shown the percent HOCl Table. This is commonly referred to as the "reservoir" effect.

3) Hypochlorite Ion

The OCl^- ion, which is a result of the dissociation phenomenon, is a relatively poor disinfectant, because of its inability to diffuse through the cell wall of microorganisms. The obstacle to this passage is the negative electrical charge, as sub-staintiated to some extent by the fact that the activation energy for disinfect ion by HOCl is in the range of those for diffusion (E = 7,000 calories), whereas that of the OCl^- ion is more characteristic of a chemical reaction (E = 15,000 calories).

It is well known that the disinfecting efficiency of free available chlorine residual decreases significantly as the pH rises. At a pH above 9 there is little disinfecting power. At this pH level and at 20^oC, 96 percent of the titrable free available chlorine will consist of the OCl^- ion. This is an indication of the low germicidal efficiency of the OCl^- ion.

In general the relative efficiencies of the OCl^- and HOCl for inactivation of cysts are summarized as follows:

4) Hypochlorite Solutions

The exact same chemical reaction occurs when hypochlorite solutions are used instead of aqueous chlorine solutions. If, for example, common bleach (sodium hypochlorite) is used, it appear in water to form hypochlorous acid:

NaOCl + H₂O <---> HOCl + NaOH

The hypochlorous acid formed by this reaction precedes to dissociate as per above reaction described in Chemistry of Hypochlorous Acid.

5) Chlorine and Nitrogenous Compounds

The most important and undoubtedly the most complex chemistry of water chlorination is its reaction with various forms of nitrogen naturally occurring in water. If the water to be treated did not contain nitrogenuous compounds, the chlorination of water would be extremely simple. The total residual would always be free available chlorine. There would be no problem with quantitative determination of residuals. The disinfecting efficiency of chlorine could be predicted and controlled within a negligible margin of error.

However, this is not the case. Nitrogen appears in most natural waters and in varying amounts as either organic or inorganic nitrogen. These compounds of nitrogen and their relationship to chlorination will be considered in the general grouping as follows:

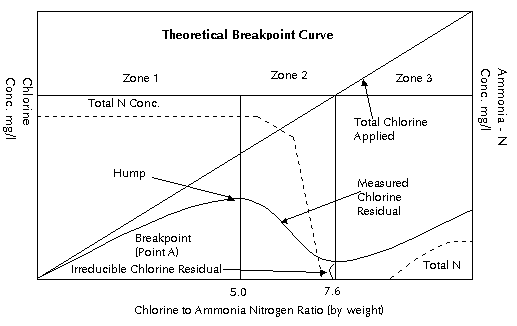
The chemical state of any nitrogen compound found in nature is a function of time in the overall life process of all plants. The amounts of these various forms of nitrogen relate directly to the sanitary quality of the water to be treated. These compounds fit very definitely in time on the nitrogen cycle of nature's own processes of purification.

The reaction of chlorine with any compound containing the nitrogen atom with one or more hydrogen atoms attached will form a compound broadly classified as an N-chloro compound, or, more commonly, as chloramine. There are two distinct classes of chloramines - organic and inorganic. The inorganic chloramines are formed by the reaction of chlorine in an aqueous solution with free ammonia naturally occurring in the water being treated. These chloramines are relatively simple compounds.

 To be continued. Please press the next button....

6) Breakpoint Phenomenon

The chemistry of this phenomenon is based on the inorganic reaction of chlorine with ammonia nitrogen. In dilute aqueous solution (1 - 50 mg/l) the reaction between ammonia nitrogen and chlorine forms three types of chloramines in the following reactions:

HOCl + NH₃ ---> NH₂Cl (monochloramine) + H₂O ------ Eq. 1
NH₂Cl + NH₃ ---> NHCl₂ (dichloramine) + H₂O ------ Eq. 2
NHCl₂ + HOCl ---> NCl₃ (trichloramiine) + H₂O ------ Eq. 3

These reactions are in general by steps, so that they all complete with each other. A series of complex reactions with all of these substances involves the chlorine substitution of each of the hydrogen atoms in the ammonia molecule. These competing reactions are grossly dependent upon pH, temperature, contact time, initial chlorine to ammonia ratio, and most of all upon the initial concentrations of chlorine and ammonia nitrogen. Note that in all three equations the chlorine atom is positively charged.

Above Eq. 1 will convert all of the free chlorine to mono chloramine at pH 7 to 8 when the ratio of chlorine to ammonia is equimolar (5:1 by weight) or less - that is, 4:1, 3:1, and so on. The rate of this reaction is extremely important, since it is pH-sensitive. According to reaction rates established by Morris, the fastest conversion of HOCl to NH₂CL occurs at pH 8.3. The following are calculated reaction rates for 99 percent conversion of free chlorine to monochloramine at 25^oC with a molar ratio of 0.2 x 10-3 mol/l HOCl and 1.0 x 10-3 mol/l NH₃:

The reaction slows appreciably as the temperature drops. At 0^oC, it requires nearly five minutes for 90 percent conversion at pH 7. The pH dependence of this reaction is described accurately on the basis of the HOCl^- OCl^- equilibrium and the NH₃- NH₄ + equilibrium.

The reaction of Eq. 2 will form dichloramine between pH and 8 if the ratio of chlorine to ammonia is 2 mol chlorine to one mol ammonia nitrogen (10:1 by weight). The rate of this reaction is much slower than that of equation 1. It may take as long as one hour for 90 percent conversion and up to five hours at pH 8.5 and above when ammonia nitrogen concentrations are very low. As the pH approaches 5 the reaction speeds up appreciably. This reaction is dependent upon pH, initial ammonia nitrogen, and temperature. The reaction time of Eq. 2 is known to be minute when the initial nitrogen concentration is in excess of 1 mg/l and pH is favorable.

The reaction of Eq. 3 will form some trichloramine (commonly called nitrogen trichloride when the pH is between 7 and 8 if the chlorine to ammonia nitrogen ratio is 3 mol of chlorine to 1 mol of ammonia nitrogen (15:1 by weight). At present very little is known about the kinetics of this reaction, particularly in concentrations of less than 10 ppm (10-4 M). Nitrogen trichloride does form, even at equimolar ratios of chlorine to ammonia nitrogen, if the pH 5, if the pH is depressed to 5 or less. At one time it was thought that it would not form above pH 5. It is known to exist in water treatment plants when the pH is as high as 9. This occurs at very high chlorine to ammonia nitrogen ratios (25:1 by weight).

In cooling water practice, if the chemistry of Eq. 1 is practiced, it is known as either the chlorine-ammonia process, the chloramine process or chloramination. Eq. 2 and 3 are related to the "breakpoint" phenomenon. It was Griffin's work which let to the discovery of this phenomenon in 1939. Grffin was attempting to explain the sudden loss of chlorine residuals and the simultaneous disappearance of ammonia nitrogen at treatment plants which were experimenting with higher than usual chlorine residuals (2 - 15 mg/l).

The breakpoint curve below is a graphic representation of chemical relationships which exist as varying amounts of chlorine are added to waters containing small amount of ammonia nitrogen. The theoretical breakpoint curve is shown in below. It was originally developed as a result of Griffin's work. This curve has several characteristic features. The principal reaction in Zone 1 is the reaction between chlorine and the ammonia ion indicated in Eq. 1. This results in a chlorine residual containing only monochloramine all the way to the hump in the curve. The hump occurs, theoretically, at a chlorine to ammonia nitrogen weight ratio of 5:1 (molar ratio 1:1). This ratio indicates the point where the reacting chlorine and ammonia nitrogen molecules are present in solution in equal numbers. As the molar ratio begins to exceed 1:1, some of the monochloramine starts a disproportionation reaction to form dichloramine in accordance with Eq. 2.

To the right of the breakpoint, Zone 3, chemical equilibria require the buildup of free chlorine residual (HOCl). In practical applications of breakpoint chlorination, reactions occur which result in the formation of nitrogen gas, nitrate, nitrogen trichloride, and other end products. These reactions consume chlorine and cause the Cl₂:NH₄ + ratio to exceed the stoichiometric value of 7.6:1 and affect the shape of the breakpoint curve.

As the chlorine to ammonia nitrogen ratio increases beyond about 12 - 15:1 the reaction of equation 3 sets in. Under these conditions the formation of nitrogen trochloride will occurs even at pH values as high as 9. As the chlorine dose is increased beyond point A in Zone 3, the free available chlorine residual will increase in an amount equal to the increase in the dosage. Therefore, the breakpoint curve in Zone 3 should plot at a 45^o angle.

It should be emphasized that the shape of the breakpoint curve is affected by contact time, temperature, concentration of chlorine and ammonia, and pH. High concentrations increase the speed of the reactions. As the pH decreases below 8.3, the reactions are retarded. The higher the temperature, the faster the reactions. The shape of the curve is different for different contact times.

In water practice this is known as free residual chlorination rather than the breakpoint process. In water treatment the practical significance of the curve is briefly as follows:

• Zone 1: The residual in this zone up to the hump are all monochloramine. The residuals in this zone do not form trichloramines.
• Zone 2: As the hump is passed, the monochloramine plus the addition of more free chlorine begins to form dichloramine, which is about twice as germicidal as monochloramine. However, this may not be the best part of the curve for the production of a palatable water.
• Zone 3: At the tip of the curve (point A) and beyond, free chlorine residual will appear. The total residual will be made up of the nuisance residuals plus free chlorine. If nitrogen trichloride is formed, it will appear in this zone. In practice it has been found that a ratio of free chlorine to total residual of 85 percent or greater will result in the most palatable water.

   

7) Alkalinity

Since chlorine solutions are highly corrosive the application of chlorine to a process stream will often raise the question of chlorine corrosion. Corrosion by chlorine is related directly to pH, which is dependent upon alkalinity. Therefore it is appropriate to know the effect of chlorine on the alkalinity of a water.

If a water is dosed with chlorine to the extent of the chlorine demand of the water, all of the chlorine applied will end up as chloride ion (Cl^-) as follows:

Cl₂ + H₂O ---> HOCl + HCl ------ Eq. 4
HOCl + Cl demand + HCl ---> 2HCl ------ Eq. 5

This calculate as 1.4 parts alkalinity for each part chlorine:

2 HCl + H₂O + CaCO₃ ---> CaCl₂ + CO₂ + 2 H₂O ------ Eq. 6
Alkalinity as CaCO₃ = 100 / Cl₂ = 100 / 71 = 1.4

The reaction in Eq. 6 occurs at pH 4.3, which is the endpoint of the alkalinity titraion, and where CO₂ exists. When HOCl is not reduced, only one Cl goes to HCl and the reaction consumes just half of the alkalinity, or 0.7. As can be seen from the above, the subject of alkalinity destruction by chlorine is not a simple one.

Take the case where water has sufficient alkalinity to maintain a 7.0 pH, and none of the chlorine applied is consumed by chlorine demand. In this case 50 percent of the chlorine applied will go to HCl. Eighty percent of the remaining 50 percent will be undissociated HOCl and unreactive in the alkalinity reactions. However, the other 20 percent of the remaining 50 percent at pH 7 is H⁺ and OCl^-.

The alkalinity reduction is calculated as follows:

50% + (0.20 x 50%) = 60%

0.6 x 1.4 = 0.84 parts alkalinity reduction by chlorine at pH 7.0. The rule of thumb for alkalinity correction by the use of caustic to maintain pH is a pound of caustic to a pound of chlorine. One part of caustic produces 1.25 parts of alkalinity. If a water at pH 7 is dosed with chlorine, and the demand is 6 mg/l, then the alkalinity reduction is 1.3 parts of alkalinity for each part of chlorine. This rule is reliable.